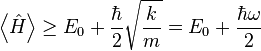Zero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature. The uncertainty principle requires every physical system to have a zero-point energy greater than the minimum of its classical potential well, even at absolute zero. For example, liquid helium does not freeze under atmospheric pressure at any temperature because of its zero-point energy.
The concept of zero-point energy was developed in Germany by Albert Einstein and Otto Stern in 1913, using a formula developed by Max Planck in 1900.[1][2] The term zero-point energy originates from the German Nullpunktsenergie.[1][2] The German name is also spelled Nullpunktenergie (without the “s”).
Vacuum energy is the zero-point energy of all the fields in space, which in the Standard Model includes the electromagnetic field, other gauge fields, fermionic fields, and the Higgs field. It is the energy of the vacuum, which in quantum field theory is defined not as empty space but as the ground state of the fields. In cosmology, the vacuum energy is one possible explanation for the cosmological constant.[3] A related term is zero-point field, which is the lowest energy state of a particular field.[4]
Contents[hide] |
[edit] History
In 1900, Max Planck derived the formula for the energy of a single energy radiator, e.g. a vibrating atomic unit:[5]
where h is Planck’s constant, ν is the frequency, k is Boltzmann’s constant, and T is the absolute temperature.
Then in 1913, using this formula as a basis, Albert Einstein and Otto Stern published a paper of great significance in which they suggested for the first time the existence of a residual energy that all oscillators have at absolute zero. They called this residual energy Nullpunktsenergie (German), later translated as zero-point energy. They carried out an analysis of the specific heat of hydrogen gas at low temperature, and concluded that the data are best represented if the vibrational energy is[1][2]
According to this expression, an atomic system at absolute zero retains an energy of ½hν.
In 1916 Walther Nernst postulated that the vacuum of space is filled with zero-point electromagnetic radiation.[citation needed]
[edit] Relation to the uncertainty principle
Zero-point energy is fundamentally related to the Heisenberg uncertainty principle. Roughly speaking, the uncertainty principle states that complementary variables (such as a particle’s position and momentum, or a field’s value and derivative at a point in space) cannot simultaneously be defined precisely by any given quantum state. In particular, there cannot be a state in which the system sits motionless at the bottom of its potential well, for then its position and momentum would both be completely determined to arbitrarily great precision. Therefore, the lowest-energy state (the ground state) of the system must have a distribution in position and momentum that satisfies the uncertainty principle, which implies its energy must be greater than the minimum of the potential well.
Near the bottom of a potential well, the Hamiltonian of a system (the quantum-mechanical operator giving its energy) can be approximated as
where E0 is the minimum of the classical potential well. The uncertainty principle tells us that
making the expectation values of the kinetic and potential terms above satisfy
The expectation value of the energy must therefore be at least
where  is the angular frequency at which the system oscillates.
is the angular frequency at which the system oscillates.
A more thorough treatment, showing that the energy of the ground state actually is 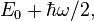 requires solving for the ground state of the system. See quantum harmonic oscillator for details.
requires solving for the ground state of the system. See quantum harmonic oscillator for details.
[edit] Varieties
The concept of zero-point energy occurs in a number of situations.
In ordinary quantum mechanics, the zero-point energy is the energy associated with the ground state of the system. The professional physics literature tends to measure frequency, as denoted by ν above, using angular frequency, denoted with ω and defined by ω = 2πν. This leads to a convention of writing Planck’s constant h with a bar through its top to denote the quantity h/2π. In those terms, the most famous such example of zero-point energy is  associated with the ground state of the quantum harmonic oscillator. In quantum mechanical terms, the zero-point energy is the expectation value of the Hamiltonian of the system in the ground state.
associated with the ground state of the quantum harmonic oscillator. In quantum mechanical terms, the zero-point energy is the expectation value of the Hamiltonian of the system in the ground state.
In quantum field theory, the fabric of space is visualized as consisting of fields, with the field at every point in space and time being a quantum harmonic oscillator, with neighboring oscillators interacting. In this case, one has a contribution of  from every point in space, resulting in a calculation of infinite zero-point energy in any finite volume; this is one reason renormalization is needed to make sense of quantum field theories. The zero-point energy is again the expectation value of the Hamiltonian; here, however, the phrase vacuum expectation value is more commonly used, and the energy is called the vacuum energy.
from every point in space, resulting in a calculation of infinite zero-point energy in any finite volume; this is one reason renormalization is needed to make sense of quantum field theories. The zero-point energy is again the expectation value of the Hamiltonian; here, however, the phrase vacuum expectation value is more commonly used, and the energy is called the vacuum energy.
In quantum perturbation theory, it is sometimes said that the contribution of one-loop and multi-loop Feynman diagrams to elementary particle propagators are the contribution of vacuum fluctuations or the zero-point energy to the particle masses.
[edit] Experimental observations
A phenomenon that is commonly presented as evidence for the existence of zero-point energy in vacuum is the Casimir effect, proposed in 1948 by Dutch physicist Hendrik B. G. Casimir (Philips Research), who considered the quantized electromagnetic field between a pair of grounded, neutral metal plates. The vacuum energy contains contributions from all wavelengths, except those excluded by the spacing between plates. As the plates draw together, more wavelengths are excluded and the vacuum energy decreases. The decrease in energy means there must be a force doing work on the plates as they move. This force has been measured and found to be in good agreement with the theory. However, there is still some debate on whether vacuum energy is necessary to explain the Casimir effect. Robert Jaffe of MIT argues that the Casimir force should not be considered evidence for vacuum energy, since it can be derived in QED without reference to vacuum energy by considering charge-current interactions (the radiation-reaction picture).[6]
The experimentally measured Lamb shift has been argued to be, in part, a zero-point energy effect.[7]
[edit] Gravitation and cosmology
| Why doesn’t the zero-point energy density of the vacuum change with changes in the volume of the universe? And related to that, why doesn’t the large constant zero-point energy density of the vacuum cause a large cosmological constant? What cancels it out? |
In cosmology, the zero-point energy offers an intriguing possibility for explaining the speculative positive values of the proposed cosmological constant. In brief, if the energy is “really there”, then it should exert a gravitational force.[8] In general relativity, mass and energy are equivalent; both produce a gravitational field. One obvious difficulty with this association is that the zero-point energy of the vacuum is absurdly large. Naively, it is infinite, because it includes the energy of waves with arbitrarily short wavelengths. But since only differences in energy are physically measurable, the infinity can be removed by renormalization. In all practical calculations, this is how the infinity is handled. It is also arguable that undiscovered physics relevant at the Planck scale reduces or eliminates the energy of waves shorter than the Planck length, making the total zero-point energy finite.
[edit] Free-energy devices
As a scientific concept, the existence of zero-point energy is not controversial although the ability to harness it is. In particular, perpetual motion machines and other power generating devices supposedly based on zero-point energy are highly controversial and, in many cases, in violation of some of the fundamental laws of physics.[citation needed] However, many engineers claim to have invented such over-unity devices.
Thus, current claims to zero-point-energy-based power generation systems have the status of pseudoscience.[9]
The discovery of zero-point energy did not alter the implausibility of perpetual motion machines. Much attention has been given to reputable science suggesting that zero-point-energy density is infinite, but in quantum theory, zero-point energy is a minimum energy below which a thermodynamic system can never go. Thus according to the standard quantum-theoretic viewpoint, none of this energy can be withdrawn without altering the system to a different form in which the system has a lower zero-point energy.
It is possible that the discovery of new physics will alter this conclusion. For example, in stochastic electrodynamics, the zero-point field is viewed as simply a classical background isotropic noise wave field which excites all systems present in the vacuum and thus is responsible for their minimum-energy or “ground” states. The requirement of Lorentz invariance at a statistical level then implies that the energy density spectrum must increase with the third power of frequency, implying infinite energy density when integrated over all frequencies.[10] If this theory is correct, there is no reason that energy, or for that matter, momentum, could not be extracted, and would of course still leave infinite energy density and infinite momentum density, isotropic in all directions simultaneously, remaining in the wave field.
According to NASA, “the concept of accessing a significant amount of useful energy from the ZPE gained much credibility when a major article on this topic was recently [March 1st, 2004] published in Aviation Week & Space Technology, a leading aerospace industry magazine”.[11]
The calculation that underlies the Casimir experiment, a calculation based on the formula predicting infinite vacuum energy, shows the zero-point energy of a system consisting of a vacuum between two plates will decrease at a finite rate as the two plates are drawn together. The vacuum energies are predicted to be infinite, but the changes are predicted to be finite. Casimir combined the projected rate of change in zero-point energy with the principle of conservation of energy to predict a force on the plates. The predicted force, which is very small and was experimentally measured to be within 5% of its predicted value, is finite.[12] Even though the zero-point energy is theoretically infinite, there is as yet no practical evidence to suggest that infinite amounts of zero-point energy are available for use, that zero-point energy can be withdrawn for free, or that zero-point energy can be used in violation of conservation of energy.[13]